Sobrepensando la temperatura de mi termo eléctrico
Sergio M. Iglesias <yo@sergio.sh>, 2026-01-09
Ah, termos eléctricos. Qué cómodos son y cuánto consumen. Aunque el nuevo que me han instalado es, de por sí, más eficiente que el anterior, le pregunté igualmente al fontanero cuál era la temperatura ideal a la que establecerlo para minimizar aún más su consumo eléctrico. Su respuesta fue un “depende”, y que vaya probando hasta sacar mis propias conclusiones. Pero aquí no hacemos las cosas así. Voy a descubrir exactamente cuál es esa temperatura según el uso que le damos en casa.
Definición del problema matemático
Los termos eléctricos son tanques de agua de volumen \(V\) cuyo contenido de líquido es siempre máximo. Esto quiere decir que, cuando gastamos agua caliente, mediante un flujo de agua hacia el exterior \(F\), también se produce un flujo igual de entrada. El agua que entra se encuentra a temperatura ambiente \(T_E\), y se mezcla con la ya presente en el termo, enfriándola. Para asegurar que la temperatura se mantiene cerca de cierto objetivo \(T_O\), el termo está dotado de un calentador con potencia \(C\) (grados/hora). Normalmente interesa tener el termo establecido a la temperatura objetivo más baja posible y que, con la mezcla de aguas del uso diario, no provoque una reducción perceptible en temperatura del agua saliente.
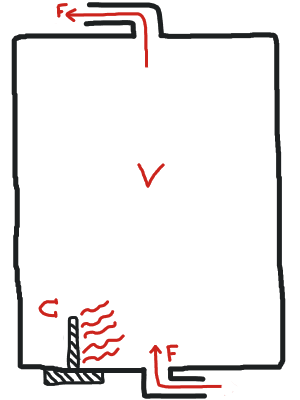
Problema: queremos encontrar la temperatura \(T_O\) a la que configurar un termo de volumen \(V\) y capacidad de calentamiento \(C\) para que, con un uso diario \(F(t)\), la temperatura del agua dentro del mismo, \(T_T(t)\), nunca caiga de los \(30\) grados.
\[\min_{t\in \{0..24\}} T_T(t) = 30\]El cambio de temperatura en el termo viene dado por la siguiente expresión:
\[\frac{dT_T(t)}{dt} = -\frac{1}{V}\frac{dF(t)}{dt}(T_T(t)-T_E(t)) + \begin{cases} C & \text{si } T_T(t) < T_O \\ 0 & \text{si no.} \end{cases}\]Que tiene dos componentes bien diferenciados: un primer término para la influencia del agua fría exterior entrante en el termo, que asume mezcla instantánea con el agua ya presente en el mismo; y un segundo término para el calentamiento del propio termo, incluyendo las pérdidas de calor.
Podemos expresar eso mismo en una ecuación discreta, mucho más útil en nuestro caso porque vamos a emplear métodos numéricos para resolverla:
\[T_T(t+\Delta t) = T_T(t) - \frac{1}{V}\frac{F(t + \Delta t) - F(t)}{\Delta t}(T_T(t)-T_E(t)) + \begin{cases} C\Delta t & \text{si } T_T(t) < T_O \\ 0 & \text{si no.} \end{cases}\]Y con consumo normal (una ducha al día y dos ciclos de lavavajillas), la función de flujo de agua (consumo) del termo es:
\[F(t) = \begin{cases} F_D \frac{T_D}{T_T(t)} & 20 \leq t < 20.25 \\ F_L \frac{T_L}{T_T(t)} & 13 \leq t < 13.5 \lor 21 \leq t < 21.5 \\ 0 & \text{si no.} \\ \end{cases}\]Esta fórmula es la única que hay que personalizar para reflejar el uso que se le da al termo. El resto son siempre iguales, aunque sus valores empíricos, como \(F_D\) (el flujo de la ducha) y \(F_L\) (el flujo del lavavajillas) sí hay que calcularlos. Para la versión discreta no necesitamos derivar esta función.
Pasemos entonces a los valores empíricos. Habrá que mojarse las manos.
Manos a la obra
Comencemos con la temperatura del agua exterior, \(T_E(t)\), que asumiremos que es constante. Basta con llenar un vaso de agua fría y medir su temperatura. Aún mejor si es invierno (para tener margen de error). En mi piso \(T_E=12\) grados centígrados.
Continuamos con el flujo de agua de la ducha, \(F_D\), para el que basta con llenar un recipiente de un litro y cronometrar el tiempo que se tarda en hacerlo, \(\Delta t\). Es mejor usar ya el agua a la temperatura que deseamos, por si esto afectase al resultado. Con eso el cálculo es muy sencillo si el termo está caliente:
\[F_D \approx \frac{1}{\Delta t}\]En mi caso \(F_D \approx 1/6\) litros por segundo, y la temperatura de la ducha \(T_D\) es de 30 grados.
El flujo del lavavajillas es más complicado, porque no podemos saber directamente cuánta agua ha usado. Sin embargo, podemos (1) desenchufar el termo para que no caliente el agua durante el experimento; (2) medir la temperatura del agua caliente antes de poner el lavavajillas, \(T_T(t_1)\); (3) la temperatura que tiene después, \(T_T(t_2)\); y (4) obtener la relación entre ambas aproximando con varios datos conocidos:
\[T_T(t_2) = T_T(t_1) + \left(T_E - T_T(t_1)\right)\frac{1}{V}F_L\frac{T_L}{T_T(t_1)}\]De ahí, despejando lo que nos interesa, obtenemos:
\[F_L = VT_T(t_1)\frac{1}{T_L}\frac{T_T(t_2) - T_T(t_1)}{T_E - T_T(t_1)}\]Ahora solo resta obtener \(C\), la capacidad para calentarse del termo, para la que debemos (1) consumir bastante agua caliente, (2) medir la temperatura \(T_1\) de un vaso de agua caliente, (3) esperar un tiempo \(\Delta t\) arbitrario, (4) medir la temperatura \(T_2\) de otro vaso de agua caliente, y (5) calcular:
\[C \approx \frac{T_2 - T_1}{\Delta t}\]Para mi termo, \(C \approx 20\), y \(F_L \approx 50\).
Visualizando los datos
Lo siguiente es un simulador interactivo que muestra la temperatura en el termo a lo largo del día con mi consumo (los dos ciclos de lavavajillas y la ducha):
Dados los valores que he medido, he decidido establecer la temperatura del termo a \(42\) grados, para dejar un pequeño margen de error en caso de que se realice otra ducha o la temperatura del agua exterior baje mucho.
Conclusiones
¿Ha bajado el consumo eléctrico de mi piso? Seguramente. ¿He perdido tanto tiempo con esto que anulo el infinitesimal beneficio económico que voy a obtener? Seguramente también. Lo cierto es que lo más fácil es hacer lo que me recomendó el fontanero, y jugar unos días con la temperatura hasta encontrar una que sea suficiente.
Por lo menos fue divertido.