:física: :historia: :matemáticas:

Si hubiera una votación para escoger la ley física más importante y de mayor profundidad, sería imposible que el principio de mínima acción no estuviese entre las opciones más populares. Este principio dicta que todo en el universo, desde las partículas más fundamentales hasta los supercúmulos galácticos, mantiene estacionario cierto valor, y a ese valor lo hemos llamado la “acción”. Es este sencillo enunciado el que precede a la mecánica clásica de Newton, la relatividad de Einstein y la mecánica cuántica, incluyendo en esta la teoría de cuerdas. En este post quiero profundizar un poco en el principio y demostrar cómo, de una simple integral, puede nacer toda física conocida.

Introducción

Dado que la materia de este post es compleja, seguiré un orden cuestionable pero –espero que– didáctico: primero definiré el concepto de acción y mínima acción, para después enseñar las ecuaciones de Euler-Lagrange sin demostrar cómo se derivan del principio, evitando que el lector sienta que el trabajo matemático requerido en dicha derivación es fútil. En un tercer apartado, realizaré la susodicha derivación paso a paso, permitiendo que el lector esté ya convencido de la utilidad de la formulación lagrangiana cuando llegue a este procedimiento. Pasaré después a demostrar que la segunda ley de Newton es consecuencia del principio de mínima acción, terminando con un repaso histórico y unas breves conclusiones.

Para hacer esto un poco más dinámico, dejo aquí una tabla de contenidos para quien quiera saltarse alguna de las secciones anteriormente mencionadas:

1. Introducción
2. La acción estacionaria
3. Las ecuaciones de Euler-Lagrange
4. Obteniendo las ecuaciones de Euler-Lagrange a partir del principio de mínima acción
5. Derivando la segunda ley de Newton de las ecuaciones de Euler-Lagrange
6. Breve historia del principio
7. Conclusiones
8. Lecturas recomendadas
9. Referencias

Tip: para saltar todas las matemáticas puede leer la introducción (1), el siguiente apartado (2), y saltar directamente al de historia del principio (6).

La acción estacionaria

La acción \(S\) es una cantidad curiosa, resultado de integrar entre dos momentos temporales \(t_1\) y \(t_2\) un valor llamado “lagrangiano”, también curioso. Cuando escribimos matemáticamente la acción, lo hacemos de la siguiente forma:

En esta ecuación encontramos notación que a aquellos profanos en física nos resulta extraña. Para empezar, tenemos \(q\), una variable que viene a representar una coordenada genérica. En coordenadas cartesianas, \(q\) podría ser \(x\), \(y\) o \(z\), mientras que en coordenadas polares podría ser el ángulo \(\phi\) o el radio \(r\), por ejemplo. Dado que queremos una fórmula apta para cualquier sistema de coordenadas y cantidad de dimensiones, usamos \(q\) como sustituto y no evitamos especificidades.

Esta \(q\) es más interesante de lo que aparenta en un primer momento, porque en realidad más que una variable es una función dependiente del tiempo, \(q(t)\), de la cual se omite el parámetro \(t\) porque es incómodo escribirlo constantemente, así que \(q = q(t)\). Esto viene a decir que la posición \(q\) varía con el tiempo \(t\), lo cual es obvio, pero fácilmente olvidable a la hora de derivar la función con respecto del tiempo. Entendemos entonces que \(q\) ya no es solo una posición en un instante \(t\) dado, porque si echamos la vista atrás y adelante en el tiempo veremos que \(q\) codifica el camino a seguir por el espacio, como se ve en la figura 1.

El siguiente elemento que podría llamarnos la atención es el punto sobre la segunda \(q\), \(\dot q\). En física, dicho punto significa que estamos tomando la derivada con respecto del tiempo, por lo que \(\dot q = \frac{d}{dt}q\), lo que nos ahorra esfuerzo mecánico al escribir las fórmulas y aún más esfuerzo cognitivo al leerlas. Nótese que \(\dot q\), al igual que \(q\), es en realidad una función del tiempo \(\dot q = \dot q (t)\), que representa la velocidad en cada momento \(t\). \(\ddot q\) sería la segunda derivada de la posición en coordenadas genéricas \(q\) con respecto del tiempo, o lo que es lo mismo, la aceleración \(\ddot q = \frac{d}{dt} \dot q = \frac{d^2}{dt^2} q = a\), que es un dato útil de recordar.

Por último, solo queda destilar qué es el lagrangiano \(\mathcal L\) para que comprendamos la ecuación anterior. Este valor no es más que el resultado de sustraer la energía potencial \(U(q)\) a la energía cinética \(T(\dot q) = \frac{1}{2}m\dot q^2\), por lo que:

Quizá lo más llamativo de \(\mathcal L\) es que las energías no se suman para obtener la energía total del sistema, sino que se le resta una a la otra para obtener una valor que no tiene equivalente natural conocido, ni es asociable a nada que podamos imaginar, demostrando que el universo y sus leyes son extraños, mucho más de lo que ya aparenta a simple vista.

Volviendo ahora a la fórmula de la acción (la integral con respecto del tiempo del lagrangiano entre dos momentos temporales), teníamos algo así:

Lo especial de esta fórmula es que, combinada con una condición que veremos en un segundo (\(\delta S = 0\)), nos revela qué camino seguirá un sistema físico entre dos momentos \(t_1\) y \(t_2\). Si lo pensamos bien, para ir de una posición \(a\) a una posición \(b\) existen infinitos caminos, desde la línea recta hasta una divagación aleatoria en miles lazos (figura 1), pero la naturaleza siempre sabe cuál escoger entre ellos. Pues bien, el camino escogido es aquel que mantiene a la acción \(S\) estacionaria (donde la primera derivada es nula):

Y es de esta ley, tan simple en su formulación (aunque compleja en sus consecuencias), de la que deriva no solo la mecánica clásica, sino que fue una precursora fundamental en el desarrollo de la relatividad general de Einstein, aunque en su caso la fórmula de la acción es distinta, llamada acción de Einstein-Hilbert. De manera similar, el principio de mínima acción es también aplicable a la mecánica cuántica, incluso cuando el concepto de “camino” en la misma es difuso, culpa de la indeterminación de Heisenberg; e incluso a la teoría de cuerdas –como ya he mencionado–, donde se usa la acción de Poliakov.

Por cierto, y para evitar futuras confusiones, llamaré a lo largo del post “acción estacionaria” a este principio, pero también “principio de Hamilton” y “principio de mínima acción”. El motivo para esta trinidad de nombres lo explicaré en la sección de historia, aunque por ahora basta con no confundirse y recordar que la acción siempre ha de ser estacionaria, no mínima, a pesar de que “mínima acción” nos lleve a pensar lo contrario.

Las ecuaciones de Euler-Lagrange

Por motivos históricos, que veremos más adelante (junto a la justificación de la trinidad de nominal), llamamos “ecuaciones de Euler-Lagrange” a unas ecuaciones que nos permiten obtener las ecuaciones del movimiento de un sistema. Estas permiten redefinir la mecánica en términos de lagrangianos, de forma similar a cómo las ecuaciones de Newton la definen como una composición de fuerzas. Donde Newton ve objetos moviéndose según el capricho de los vectores, Euler y Lagrange vieron campos de energía potencial que trazan sus caminos a seguir:

Estas ecuaciones no deben tomarse a la ligera, pues estableciendo adecuadamente el lagrangiano y resolviendo las derivadas se pueden obtener ecuaciones del movimiento de cualquier sistema físico clásico (no relativista ni cuántico). Comprobemos esto con una aplicación práctica: un muelle. En este caso, la energía cinética es la típica, y la potencial es \(U(x) = \frac{1}{2}kx^2\), donde \(k\) representa la eslasticidad de nuestro muelle. Sabiendo esto, podemos definir el lagrangiano como:

Y poniendo dicho \(\mathcal L\) en las ecuaciones de Euler-Lagrange, y resolviendo las derivadas, obtenemos:

Que es una ecuación diferencial de segundo orden que describe el movimiento de un muelle en una dimensión. Si ahora introducimos dicha fórmula en un simulador físico (simulador 1), podemos observar al muelle oscilar de izquierda a derecha, con su velocidad de oscilación siendo dependiente de los parámetros de masa \(m\) y elasticisdad \(k\).

figure 1

Si nuestro muelle unidimensional estuviese afectado por la fuerza de la gravedad, habría que añadir un nuevo término al lagrangiago que represente la energía potencial de la atracción, \(U_g = mgz\). Esta nueva energía potencial asume que el elongamiento del muelle no causa cambios en la atracción gravitatoria, que podría suceder con un muelle kilométrico, en cuyo caso tendríamos que recalcular \(g\) en cada instante (\(g(z)=\frac{GM}{z^2}\)). En este nuevo lagrangiano llamaré \(z\) y no \(x\) a la posición para imaginar que el muelle es vertical:

Y resolviendo otra vez tenemos una nueva ecuación del movimiento:

Que traducida a código nos resulta en el simulador 2, muy similar al primero pero con un nuevo parámetro \(g\).

Si bien hemos empleado las ecuaciones de Euler-Lagrange para resolver el movimiento de sistemas simples, también podemos usarlas en otros más complejos, donde creo que destacan especialmente. Es el caso del péndulo, para el cual solo tenemos que definir su posición en coordenadas polares y lo demás casi se resuelve solo, porque al decir que la velocidad dependerá de la velocidad angular y la longitud de la cuerda \(l\dot \theta\), y que la altura (necesaria para calcular el potencial gravitatorio) es \(l(1-\cos\theta)\), tenemos el siguiente lagrangiano:

Que al introducirlo en las ecuaciones de Euler-Lagrange nos devuelve una fórmula elegantísima:

Y para esta fórmula he preparado el simulador 3, que muestra el péndulo funcionando correctamente.

Pensemos un momento en lo que acabamos de hacer. En la mecánica de Newton nos habríamos visto obligados a identificar las fuerzas presentes en el péndulo (gravedad, tensión, etc.) y, a su vez, tendríamos que calcular para cada una de ellas su valor, identificando aquellas cuyos componentes se cancelan. Sin embargo, usando el método lagrangiano solo necesitamos definir \(\mathcal L\), y todo lo demás ya es solo álgebra.

Como hemos visto, el péndulo es una buena muestra de la sencillez con la que el método lagrangiano permite describir (¡Y simular!) sistemas físicos, pero desde luego no la única. En el lagrangiano mostrado a continuación se codifica un sistema gravitatorio de dos dimensiones con varias masas \(i\), cada una con su posición (\(x_i\) e \(y_y\)), su masa (\(m_i\)) y su lagrangiano (\(\mathcal L_i\)). Cada uno de estos objetos se ve atraído por todos los demás, lo que implica que el potencial total es la suma de los potenciales gravitatorios de cada par \(i,j\) con \(i \neq j\).

Repetimos proceso de introducir el lagrangiano en las ecuaciones de Euler-Lagrange para obtener las siguientes ecuaciones del movimiento:

Y ahora codifico esas fórmulas resultando en el simulador 3, donde ofrezco tres simulaciones diferentes: objetos en caída libre, un planeta con su luna orbitando una estrella y un sistema estelar binario. Nótense dos cosas, primero que he introducido en la simulación una fuerza de repulsión cuando los objetos colisionen, segundo que los parámetros de distancia y velocidad están establecidos a ojímetro, y por lo tanto las órbitas no son estables, por lo que recomiendo pulsar sobre los botones para reiniciar la simulación, seguramente rota tras estar corriendo durante más de dos minutos.

Vamos a terminar con un último ejemplo, para el que no proporcionaré un simulador: un sistema gravitacional con colisiones reales entre los objetos, no con un parche como el que hice en el caso anterior. Lo dejo como un problema abierto porque no lo he solucionado antes de escribir este post, por motivos que diré más adelante. En este sistema, el lagrangiano es el siguiente, muy similar al anterior, pero con un nuevo término que genera un muro de potencial entre los dos objetos:

En este caso \(E\) es un parámetro que indica la intensidad del muro de potencial que previene la colisión. Valoré introducir el límite \(E\rightarrow \infty\) para que el muro fuera perfectamente vertical pero, aparte de poco natural, sería problemático de codificar, por lo que se quedó sin él. Con todo esto establecido, obtenemos las ecuaciones de movimiento:

Y estas, al ser introducidas en un simulador, provocan que los objetos se lancen a altísimas velocidades en todas las direcciones. La teoría principal que barajo actualmente es que, dado que el simulador tiene que ser necesariamente discreto (y esa discreción introduce errores de predicción) los objetos están entrando en contacto, superponiéndose unos con los otros y escalando más de lo debido en el muro de potencial, lo que les hace ganar energía sin precedentes que los lleva a aceleraciones y velocidades de decenas de dígitos. La solución seguramente sería calcular varios pasos intermedios de un movimiento antes de realizarlo, una técnica común en videojuegos que se remonta, como mínimo, al Super Mario 64, pero esto es trabajo para el lector.

Obteniendo las ecuaciones de Euler-Lagrange a partir del principio de mínima acción

Ahora que ya hemos visto en qué consiste el principio de mínima acción (¡Acción estacionaria!) y hemos empleado las ecuaciones de Euler-Lagrange para definir el movimiento de varios sistemas físicos, vamos a proceder a obtener estas mismas ecuaciones a partir del principio, demostrando que no son más que una consecuencia del mismo. El método que usaremos será igual al que Hamilton empleó en su momento para hacer el proceso, basado en el cálculo de variaciones inventado por Lagrange años antes y del cual hablaré en más detalle en la sección de historia.

Primero, asumamos que \(q\) es el camino correcto que nuestro sistema va a seguir. Introduzcamos una perturbación \(\eta: \mathbb R\rightarrow \mathbb R\) que altere nuestro camino original \(q\) y cuyo efecto sobre este será modulado por un escalar \(\varepsilon\), dejándonos con un nuevo camino, una variación:

El nuevo \(\eta\) será dependiente del tiempo, y cumplirá que \(\eta(t_1) = \eta(t_2) = 0\) para que \(\varrho\) y \(q\) comiencen y terminen en el mismo lugar, es decir, que sean caminos alternativos entre ambos puntos, como se ve en la figura 2. Obviamente, \(\eta\) ha de ser derivable en el intervalo \([t_1, t_2]\), antes de que los lectores matemáticos me crucifiquen por no especificarlo.

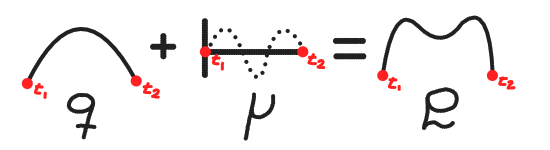
Con eso establecido, el lagrangiano del camino alterado \(\varrho\) se nos queda como:

Y ese lagrangiano podemos, a su vez, ponerlo en la fórmula de la acción:

Derivamos \(I\) con respecto de \(\varepsilon\) y obtenemos lo siguiente:

Resolvemos la segunda mitad (\(\int_{t_1}^{t_2} \dot \eta \frac{\partial}{\partial \dot \varrho} \mathcal L(\varrho, \dot \varrho) dt\)) usando integración por partes con \(u = \frac{\partial}{\partial \dot \varrho} \mathcal L(\varrho, \dot \varrho)\) y \(\dot v = \dot \eta\):

Pero como \(\eta(t_0) = \eta(t_1) = 0\), en la fórmula anterior la parte anterior a la integral desaparece, dejándonos solo con:

Y esta ya podemos devolverla a la integral completa anterior , la fórmula de \(\frac{\partial}{\partial \varepsilon}I\), porque ahora sabemos que \(\int_{t_1}^{t_2} \dot \eta \frac{\partial}{\partial \dot \varrho} \mathcal L(\varrho, \dot \varrho)dt = - \int_{t_1}^{t_2} \eta \frac{d}{dt} \frac{\partial}{\partial \dot \varrho} \mathcal L(\varrho, \dot \varrho) dt\):

Y ahora evaluamos la función en \(\varepsilon = 0\), quitando así la perturbación \(\varepsilon \eta\) que habíamos introducido originalmente, que nos deja con \(\varrho = q\), y buscamos que el valor sea estacionario, igual a cero, que tiene que darse para ese \(\varepsilon = 0\):

Y aplicamos el lema fundamental del cálculo de variaciones: \(\eta(t)\) tiene un valor arbitrario. La única forma de que esto sea cierto es que el contenido de los corchetes sea cero, porque \(t_1\) y \(t_2\) son también arbitrarios y siempre podríamos escogerlos de tal forma que la integral resultara distinta a cero si esa condición no se diese, dejándonos con la fórmula de abajo.

Que son las ecuaciones de Euler-Lagrange para una dimensión, aunque con signo opuesto a como las hemos estado utilizando en el apartado anterior. Quod erat demonstrandum.

Derivando la segunda ley de Newton de las ecuaciones de Euler-Lagrange

Lo único que me queda por demostrar es que las ecuaciones de Euler-Lagrange, la aproximación lagrangiana de la mecánica clásica, son una reformulación de la mecánica de Newton. Para ello, hay que partir de las ya conocidas ecuaciones:

En estas, vamos a sustituir el lagrangiano \(\mathcal L\) por su valor, \(T(\dot q) - U(q)\), observando que la energía cinética no depende de la posición, ni la potencial de la velocidad, por lo que \(\frac{\partial}{\partial q}T(\dot q) = \frac{\partial}{\partial \dot q}U(q) = 0\):

Ahora sustituimos \(T\) por su valor (\(\frac{1}{2}m\dot q^2\)) y recordamos que \(-\frac{\partial}{\partial q} U(q)\) es la fuerza, porque por definición una fuerza es el gradiente negativo del potencial, lo que nos lleva a:

Que no deja de ser una reformulación de la segunda ley de Newton, la ley fundamental de la dinámica:

Por lo que ambas aproximaciones a la física son equivalentes, siempre que no tengamos casos extraños no contemplados por Newton, como potenciales dependientes de la velocidad. Podemos interpretar esta equivalencia como se muestra en la figura 3: mientras que las leyes de newton nos describen las fuerzas que actúan en el sistema en un momento dado, el principio de acción estacionaria nos dice el camino que este sigue en todo momento. El camino seguido ha de ser aquel indicado por las fuerzas, y las fuerzas aquellas que produzcan dicho camino, dos caras de la misma moneda.

Breve historia del principio

Ignorando formulaciones extremadamente primitivas, la historia del principio de mínima acción (¡Acción estacionaria!) comienza, posiblemente, en la mente de Leibniz (uno de los dos padres del cálculo infinitesimal), aunque la fuente primaria de este supuesto descubrimiento, una carta de 1707, se ha perdido [1]. Una definición clara del principio no llegaría hasta Maupertuis, quien en sus estudios de óptica durante 1744 dijo que “la luz ha de tomar la decisión de si seguir el camino de menor distancia […] o el de menor tiempo. […] La luz no puede pasar por ambos a la vez, entonces, ¿cómo decide tomar uno o el otro? En vez de tomar uno de estos caminos per se, la luz toma el camino que ofrece una ventaja real: la luz toma el camino que minimiza su acción”. Tras esta revelación, el físico nos define a qué se refiere precisamente con “acción”: “[…] es la suma proporcional de las distancias viajadas multiplicadas por sendas velocidades de cada tramo” [2]. Desde luego la definición es primitiva, y Maupertuis solo pretende aplicarla a la luz, no a cualquier cuerpo en movimiento (“La acción es el verdadero gasto de la naturaleza, que esta logra hacer tan pequeño como sea posible en el movimiento de la luz”, cursiva propia), pero es un paso adelante en abstracción con respecto a sus coetáneos como Fermat, quien pensaba que “el camino entre dos puntos tomado por un rayo de luz es el que es recorrido en un tiempo menor” [3].

Sospecho, por cierto, que el nombre de “principio de mínima acción” viene de Maupertuis, porque fue él la última referencia que encuentro que habla de “mínimos” y no de “puntos estacionarios” (mínimos, máximos y sillas). Es por este malentendido en las primeras formulaciones del principio el que hace que aún a día de hoy le llamemos así y no de la forma correcta: “principio de acción estacionaria”.

Siguiendo con la historia, casi simultáneamente a Maupertuis definió Euler la acción como la integral con respecto del tiempo del producto masa-velocidad, que siendo la primera constante se queda como \(M\int vdt\), y aplicando el principio a todo tipo de problemas mecánicos, no solo de óptica [4][5]. Si bien Euler fue primero en dar una definición de la acción, este nunca reclamó prioridad en el descubrimiento, e incluso defendió a Maupertuis cuando Samuel König, un matemático alemán, le acusó de plagiar el trabajo de Leibniz en aquella carta perdida de 1707. El lío causado no fue pequeño, pues König no tenía la carta original (ya perdida en esos tiempos) sino una copia de la misma, y se le condenó por falsificación, especialmente por “usa[r] el nombre de un gran hombre [Leibniz], que como sabemos, es respetado por toda Europa […]”. Parece que con el tiempo la Academia de Berlín ha cambiado su opinión en el asunto, y ha concluido que la carta tuvo que existir, dándole la razón a König después de 150 años [2].

Volviendo a Euler, lo que él buscaba era aplicar este principio para resolver el problema de la curva isócrona, una superficie sobre la cual siempre se tarda la misma cantidad de tiempo en deslizarse hasta el final, independientemente de dónde se empiece. Euler atacó el problema equipado con su principio de mínima acción y un rudimentario cálculo de variaciones, falto de una definición formal [6].

En el verano de 1754 recibiría Euler una carta de un jovencísimo matemático turinés de 17 años, Joseph Louis de Lagrange, que quedaría sin responder a juzgar por el archivo histórico. No sucedería lo mismo con la segunda carta del joven, enviada en agosto del siguiente año, que impresionaría tanto a Euler que la correspondencia entre ambos genios se extendería veinte años [7]. En esa carta estival, Lagrange presentaba el cálculo de variaciones de manera puramente analítica, frente a la presentación geométrica que Euler había desarrollado. Euler estaba sorprendido, y rápidamente adoptó el nuevo formalismo en sus soluciones, que es el mismo que hemos utilizado en apartados superiores al sustituir el camino \(q\) por una variación del mismo, \(\varrho = q + \varepsilon\eta\), y después resolver para \(\varepsilon=0\). Lagrange no solo apoyó a Euler, pues siguió investigando el principio tras la muerte de su maestro, logrando grandes avances independientes en el estudio de la mecánica [8].

La última pieza del puzzle la puso Hamilton, al derivar las ecuaciones de Euler-Lagrange mediante el cálculo de variaciones y dar la forma definitiva a la acción, \(\mathcal L(q, \dot q) = T(\dot q) - U(q)\) [9], que es la que hemos usado a lo largo del post. Por su contribución, se llamó “principio de Hamilton” a esta variante del principio de acción estacionaria, y es uno de los títulos que barajé para este texto: “sobre el principio de Hamilton”. Con el tiempo sería este principio el que se demostraría superior frente a la mecánica de vectores de Newton en campos como el electromagnetismo, e indispensable para la nueva física dual del siglo XX.

Hamilton no es solo padre de la actual formulación Lagrangiana, también concebió la formulación Hamiltoniana, con la cual uno puede obtener ecuaciones del movimiento alternativas en forma de ecuaciones diferenciales más sencillas (de primer orden), so pena de duplicar la cantidad de ecuaciones. También es por su culpa gracias a él que la acción recibe el nombre de \(S\) y no \(A\), ya que seguramente empleaba esa letra como representación des-estilizada del símbolo integral.

Conclusiones

La formulación lagrangiana de la mecánica clásica nos da las herramientas para entender la física desde un ángulo que Newton no había contemplado, un ángulo tan elegante como sencillo. La aproximación de Euler, Lagrange y Hamilton es otra herramienta más en el cajón de sastre del físico que, aunque no sustituye a su contraparte Newtoniana en los problemas más sencillos, es especialmente dotada en sistemas complejos y con coordenadas no-cartesianas. Su desarrollo ha permitido buena parte de los avances de esta ciencia, y es muy probable que las futuras innovaciones y descubrimientos sigan apoyándose esta famosa integral.

Lecturas recomendadas

El capítulo 19 del segundo volumen de las clases de física de Richard Feynman ofrece una muy buena introducción al tema de este post. También lo hace el libro “The theoretical minimum” de Leonard Suskind, aunque ninguno de los dos entra en la historia del principio. Esa laguna la cubren este paper y este post de Scholarpedia, que son las únicas fuentes que he encontrado que tratan el asunto con más profundidad que yo aquí.

Referencias

1. [1]J. J. O’Connor y E. F. Robertson, «The Berlin Academy and forgery», MacTutor. abr. 2003, [En línea]. Disponible en: https://mathshistory.st-andrews.ac.uk/HistTopics/Forgery_2/.

2. [2]Pierre Louis Moreau de Maupertuis, «Accord between different laws of Nature that seemed incompatible». 1744, [En línea]. Disponible en: https://en.wikisource.org/wiki/Translation:Accord_between_different_laws_of_Nature_that_seemed_incompatible.

3. [3]R. E. Bradley y C. E. Sandifer, Eds., Leonhard Euler: life, work, and legacy, 1St ed., n.º v. 5. Amsterdam ; Boston: Elsevier, 2008.

4. [4]Leonhard Euler, Methodus inveniendi traiectorias reciprocas algebraicas, n.º 3. Euler Archive, 1727.

5. [5]Leonhard Euler, «Methodus inveniendi/Additamentum II», Wikisource. 1744, [En línea]. Disponible en: https://la.wikisource.org/wiki/Methodus_inveniendi/Additamentum_II.

6. [6]C. Gray, «Principle of least action», Scholarpedia, vol. 4, n.º 12, p. 8291, 2009, doi: 10.4249/scholarpedia.8291.

7. [7]Euler Archive, «Euler’s Correspondence with Joseph Louis de Lagrange», Euler Archive. [En línea]. Disponible en: http://eulerarchive.maa.org/correspondence/correspondents/Lagrange.html.

8. [8]Joseph-Louis Lagrange, Mécanique analytique, vol. 2. 1788.

9. [9]William Rowan Hamilton, «ON A GENERAL METHOD IN DYNAMICS», Philosophical Transactions of the Royal Society, vol. part II for 1834, pp. 247-308, mar. 1834, [En línea]. Disponible en: https://www.maths.tcd.ie/pub/HistMath/People/Hamilton/Dynamics/GenMeth.pdf.